Đề thi thử đánh giá tư duy ĐH Bách khoa Hà Nội số 5 có đáp án - Tuyensinh247

CẤU TRÚC BÀI THI

-----------------------------------------

NỘI DUNG BÀI THI

BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM

PHẦN I: TƯ DUY TOÁN HỌC

Câu 1: Công thức tính diện tích toàn phần hình nón có bán kính đáy \(r\), độ dài đường cao \(h\) và độ dài đường sinh \(l\) là:

A. \({S_{tp}} = \pi rl + \pi {r^2}\)

B. \({S_{tp}} = \pi rl + 2\pi {r^2}\)

C. \({S_{tp}} = \pi rh + \pi {r^2}\)

D. \({S_{tp}} = 2\pi rh\) 

Câu 2: Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ bên. Giá trị cực đại của hàm số là?

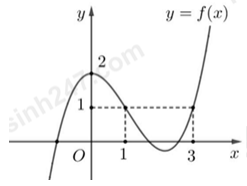
A. \(y = 0\). 

B. \(y = 2\).

C. \(y = 1\). 

D. \(y = 3\).

Câu 3: Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A(3;2; - 1),B(5;4;3)\). \(M\) là điểm thuộc tia đối của tia \(BA\) sao cho \(\dfrac{{AM}}{{BM}} = 2\). Tìm tọa độ của điểm \(M\).

A. \((7;6;7)\).

B. \(\left( {\dfrac{{13}}{3};\dfrac{{10}}{3};\dfrac{5}{3}} \right)\).

C. \(\left( { - \dfrac{5}{3}; - \dfrac{2}{3};\dfrac{{11}}{3}} \right)\).                        

D. \((13;11;5)\).

Câu 4: Cho cấp số cộng \(({u_n})\) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}{{u_1} + {u_7} = 26}\\{u_2^2 + u_6^2 = 466}\end{array}} \right.\). Mệnh đề nào sau đây đúng?

A. \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 13}\\{d = {\rm{\;}} - 3}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 10}\\{d = {\rm{\;}} - 3}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{d = 4}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 13}\\{d = {\rm{\;}} - 4}\end{array}} \right.\).

Câu 5: Cho hai số phức \({z_1} = 2 - i\) và \({z_2} = {\rm{\;}} - 3 + 5i\). Điểm biểu diễn số phức \(w = 3{z_1} - i.\overline {{z_2}} \) có hoành độ bằng………

Câu 6: Viết phương trình mặt phẳng \((\alpha )\) đi qua \(M(0;1;2),N(2;0;1)\) và vuông góc với \((P)\): \(2x + 3y - z + 1 = 0\)

A. \(x + 2z - 4 = 0.\)

B. \(x + 2y - 4 = 0.\)

C. \(y + 3z - 2 = 0\). 

D. \(x - 2z - 4 = 0.\)

Câu 7: Trong không gian \({\rm{Ox}}yz\), cho các mặt phẳng \((P):x - y + 2z + 1 = 0\), \((Q):2x + y + z - 1 = 0\). Gọi \((S)\) là mặt cầu có tâm thuộc trục hoành, đồng thời \((S)\) cắt mặt phẳng \((P)\) theo giao tuyến là một đường tròn có bán kính 2 và \((S)\) cắt mặt phẳng \((Q)\) theo giao tuyến là một đường tròn có bán kính \(r\). Để chỉ có đúng 1 mặt cầu \((S)\) thỏa mãn yêu cầu thì giá trị của \(r\) là

A. \(\sqrt 3 \).

B. \(\sqrt 2 \). 

C. \(\sqrt {\dfrac{3}{2}} \). 

D. \(\dfrac{{3\sqrt 2 }}{2}\).

Câu 8: Người ta cần tạo một ống bơ sữa đặc kín 2 đầu hình trụ có đáy là hình tròn với thể tích là \(16\pi c{m^3}\). Tính diện tích tối ưu của phần vật liệu cần sử dụng.

A. \(24\pi \left( {c{m^2}} \right)\) 

B. \(23\pi \left( {c{m^2}} \right)\)

C. \(21\pi \left( {c{m^2}} \right)\) 

D. \(20\pi \left( {c{m^2}} \right)\)

Câu 9: Cắt hình trụ \(\left( T \right)\) bằng một mặt phẳng song song với trục và cách trục \(2{\mkern 1mu} {\rm{m}}\) được thiết diện là một hình vuông có diện tích bằng \(16{\mkern 1mu} {{\rm{m}}^2}\). Tính thể tích của khối trụ \(\left( T \right)\).

A. \(32\pi \left( {{m^3}} \right)\)

B. \(16\pi \left( {{m^3}} \right)\)

C. \(64\pi \left( {{m^3}} \right)\) 

D. \(8\pi \left( {{m^3}} \right)\)

Câu 10: Trong không gian Oxyz, cho điểm \(A\left( {1;2;4} \right)\) và hai đường thẳng \({d_1}:{\mkern 1mu} {\mkern 1mu} \dfrac{x}{1} = \dfrac{y}{1} = \dfrac{z}{1},\) \({d_2}:{\mkern 1mu} \left\{ {\begin{array}{*{20}{l}}{x = 1 - t}\\{y = 1 + t}\\{z = 2t}\end{array}} \right..\) Đường thẳng \(\Delta \) qua A, vuông góc với \({d_1}\) và cắt \({d_2}\) có phương trình là  

A. \({\mkern 1mu} {\mkern 1mu} \dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{1} = \dfrac{{z - 4}}{{ - 2}}.\) 

B. \(\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y - 2}}{1} = \dfrac{{z - 4}}{2}.\)

C. \(\dfrac{{x + 1}}{{ - 5}} = \dfrac{{y + 2}}{3} = \dfrac{{z + 4}}{2}.\)

D. \(\dfrac{{x - 1}}{{ - 5}} = \dfrac{{y - 2}}{3} = \dfrac{{z - 4}}{2}.\)

Câu 11: Trong không gian Oxyz, tọa độ điểm A' là hình chiếu vuông góc của điểm \(A\left( { - 1;4;0} \right)\) lên mặt phẳng \(\left( {\alpha {\rm{ \;}}} \right):x - 2y + 4z + 10 = 0\) là

A. \(A'\left( { - \dfrac{{86}}{{21}};\dfrac{{22}}{{21}}; - \dfrac{4}{{21}}} \right)\). 

B. \(A'\left( { - 22;86; - 4} \right)\).

C. \(A'\left( {\dfrac{4}{{21}}; - \dfrac{{86}}{{21}}; - \dfrac{{22}}{{21}}} \right)\). 

D. \(A'\left( { - \dfrac{{22}}{{21}};\dfrac{{86}}{{21}}; - \dfrac{4}{{21}}} \right)\).

Câu 12: Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:

Giới hạn \(I = \mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \sqrt {{x^6} + 5x - 1} \) bằng………

Câu 13: Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê, và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm 2 căn hộ bị bỏ trống. Hỏi để có thu nhập cao nhất, công ti đó phải cho thuê mỗi căn hộ với giá tiền là bao nhiêu một tháng? (đồng/tháng)

A. 2 250 000. 

B. 2 450 000.

C. 2 300 000.

D. 2 225 000.

Câu 14: Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Các khẳng định sau đúng hay sai?

Câu 15: Cho tam giác ABC vuông tại \(A\) có \(AB = 6{\mkern 1mu} cm,{\mkern 1mu} AC = 8{\mkern 1mu} cm\). Thể tích khối tròn xoay thu được khi quay tam giác ABC quanh trục BC là

A. \(\dfrac{{96}}{5}\pi \).

B. \(\dfrac{{128}}{5}\pi \).

C. \(\dfrac{{1152}}{5}\pi \).

D. \(\dfrac{{384}}{5}\pi \).

Câu 16: Cho hai số phức \({z_1},{z_2}\) thỏa mãn đồng thời hai điều kiện sau \(\left| {z - 1} \right| = \sqrt {34} ,\left| {z + 1 + mi} \right| = \left| {z + m + 2i} \right|\) (trong đó \(m\) là số thực) và sao cho \(\left| {{z_1} - {z_2}} \right|\) là lớn nhất. Khi đó giá trị \(\left| {{z_1} + {z_2}} \right|\) bằng

A. \(\sqrt 2 \).

B. 10.

C. \(2\).

D. \(\sqrt {130} \)

Câu 17: Điền số thích hợp vào chỗ trống:

Điểm đối xứng của điểm \(M( - 2;3;4)\) qua mặt phẳng \((Oxy)\) là điểm M' có cao độ bằng …………

Câu 18: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \({A^\prime },{B^\prime },{C^\prime }\) sao cho \(SA = 2S{A^\prime };SB = 3S{B^\prime };SC = 4S{C^\prime }\), mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }} \right)\) cắt cạnh \(SD\) tại \({D^\prime }\). Gọi \({V_1},{V_2}\) lần lượt là thể tích của hai khối chóp \(S.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) và \(S.ABCD\). Khi đó tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng:

A. \(\dfrac{1}{{24}}\).

B. \(\dfrac{1}{{26}}\).

C. \(\dfrac{7}{{12}}\).

D. \(\dfrac{7}{{24}}\).

Câu 19: Cho tam giác ABC đều cạnh bằng \(4\). Gọi \(M,{\mkern 1mu} N\) lần lượt là trung điểm \(AB,{\mkern 1mu} AC\). Diện tích đa giác thu được khi lấy đối xứng tam giác ABC qua trục MN là \(a\sqrt b \) \((a,b \in \mathbb{Z})\). Trong các phát biểu sau, phát biểu nào đúng?

A. \(a\) chia hết cho \(b\).

B. \(a - 2b = 1\).

C. \(a + 2b\) chia hết cho \(5\).

D. \(a + b\) là số chính phương.

Câu 20: Cho các mệnh đề sau:

I/ Số cạnh của một khối đa diện lồi luôn lớn hơn hoặc bằng 6.

II/ Số mặt của khối đa diện lồi luôn lớn hơn hoặc bằng 5.

III/ Số đỉnh của khối đa diện lồi luôn lớn hơn 4.

Trong các mệnh đề trên, những mệnh đề nào là mệnh đề đúng?

A. II và III.

B. I và II.

C. Chỉ I.

D. Chỉ II.

Câu 21: Ta gọi số nguyên bé nhất không nhỏ hơn \(x\) là phần nguyên trên của \(x\), kí hiệu \(\left\lceil x \right\rceil \). Chằng hạn \(\left\lceil { - 2,5} \right\rceil {\rm{\;}} = {\rm{\;}} - 2;{\mkern 1mu} \left\lceil {\dfrac{{19}}{6}} \right\rceil {\rm{\;}} = 4\).

Tổng phần nguyên trên của tất cả các số có dạng \(\dfrac{k}{3}\) với \(k\) nguyên lấy giá trị từ \( - 5\) đến \(5\) bằng ………

Câu 22: Một hộp chứa \(5\) viên bi màu trắng, 15 viên bi màu xanh và 35 viên bi màu đỏ. Lấy ngẫu nhiên từ hộp ra \(7\) viên bi. Xác suất để trong số \(7\) viên bi được lấy ra có ít nhất \(1\) viên bi màu đỏ là:

A. \(C_{35}^1.\)

B. \(\dfrac{{C_{55}^7 - C_{20}^7}}{{C_{55}^7}}.\)

C. \(\dfrac{{C_{35}^7}}{{C_{55}^7}}.\)

D. \(C_{35}^1.C_{20}^6.\)

Câu 23: Biết hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

Các khẳng định sau là đúng hay sai?

Câu 24: Gọi \({z_1},{\mkern 1mu} {z_2}\) là nghiệm của phương trình \({z^2} + 4z + 5 = 0\). Tính giá trị của biểu thức \(P = \dfrac{{z_1^2}}{{{z_2}}} + \dfrac{{z_2^2}}{{{z_1}}}\).

A. \(\dfrac{4}{5}\).

B. \( - \dfrac{4}{5}\).

C. \( - \dfrac{4}{{25}}\).

D. \( - \dfrac{8}{5}\).

Câu 25: Một vận động viên đang luyện tập chạy đường dài, dự định buổi tập hôm nay sẽ chạy trong 50 phút. Trong vòng 15 phút đầu tiên người vận động viên chạy với vận tốc \(10km/h\), do có sự suy giảm thể lực nên mỗi 10 phút tiếp theo vận tốc của người vận động viên giảm so với trước đó \(1km/h\). Hỏi đến khi hoàn thành buổi tập thì người vận động viên đã chạy được quãng đường là bao nhiêu?

A. 9km.

B. 8km.

C. 7km.

D. 6km.

Câu 26: Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:

A. 35.

B. 120.

C. 240.

D. 720.

Câu 27: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

Câu 28: Khai triển nhị thức \({\left( {x + 2} \right)^{n + 5}}{\mkern 1mu} {\mkern 1mu} \left( {n \in \mathbb{N}} \right)\) có tất cả 2019 số hạng. Tìm \(n\).

A. 2018.

B. 2014.

C. 2013.

D. 2015.

Câu 29: Gọi \(S\) là tổng các nghiệm của phương trình \({9^{\dfrac{x}{2}}} + 9.{\left( {\dfrac{1}{{\sqrt 3 }}} \right)^{2x + 2}} - 4 = 0\). Khi đó \(S\) thuộc những khoảng nào trong các khoảng dưới đây?

A. \(( - 1;1)\).

B. \((0;2)\).

C. \(\left( { - \dfrac{1}{2};\dfrac{3}{2}} \right)\). 

D.  \(\left( { - 2;0} \right)\).

Câu 30: Dãy số Phi-bô-na-xi là dãy số \(({u_n})\) được xác định như sau: \({u_1} = {u_2} = 1;{u_n} = {u_{n - 1}}{\rm{\;}} + {u_{n - 2}}\) với \(n{\rm{\;}} \ge \)3. Số hạng thứ 11 của dãy số Phi-bô-na-xi là

A. 44.

B. 55.

C. 89.

D. 144.

Câu 31: Cho tứ diện \(ABCD\) có thể tích \(V\) với \(M,\;N\) lần lượt là trung điểm \(AB,\;CD\). Gọi \({V_1},\;{V_2}\) lần lượt là thể tích của \(MNBC\) và \(MNDA\). Tỉ lệ \(\dfrac{{{V_1} + {V_2}}}{V}\) bằng

A. \(\dfrac{2}{3}\).

B. \(\dfrac{1}{2}\).

C. \(\dfrac{1}{3}\).

D. \(\dfrac{3}{2}\).

Câu 32: Cho hàm số \(y = \left| {{x^4} - 2m{x^2} + 2m - 1} \right|\) với \(m\) là tham số thực. Số giá trị nguyên trong khoảng \(\left[ { - 2;2} \right]\) của \(m\) để hàm số đã cho có \(3\) điểm cực trị là

A. 3.

B. 2.

C. 1.

D. 4.

Câu 33: Một vật chuyển động trong 3 giờ với vận tốc \(v(km/h)\) phụ thuộc vào thời gian \(t(h)\) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như hình bên. Quãng đường \(s(km)\) mà vật di chuyển được trong 3 giờ là?

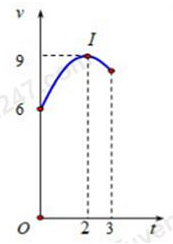
A. 25,25.

B. 24,25.

C. 24,75.

D. 26,75.

Câu 34: Hàm số \(y = {x^4} - 2{x^2} + 1\) nghịch biến trên khoảng nào dưới đây?

A. \(\left( { - 1;1} \right)\).

B. \(\left( { - 1;0} \right)\).

C. \(\left( { - \infty ;1} \right)\).

D. \(\left( { - \infty ; - 1} \right)\).

Câu 35: Đồ thị hàm số \(y = \dfrac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}}\)có bao nhiêu đường tiệm cận đứng và ngang?

A. 2.

B. 1.

C. 3. 

D. 4

Câu 36: Cho hàm số \(y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + \left( {m - 3} \right)x + \dfrac{9}{2}\) (m là tham số thực). Có bao nhiêu giá trị nguyên của m thuộc [-5;5] để hàm số đã cho cắt đường thẳng \(y = {\rm{ \;}} - 3x + \dfrac{9}{2}\) tại 3 điểm phân biệt?

A. 9.

B. 7. 

C. 6.

D. 5

Câu 37: \(A,B\) là hai số tự nhiên liên tiếp thỏa mãn \(A < \dfrac{{{2^{2021}}}}{{{3^{1273}}}} < B\). Giá trị \(A + B\) là

A. 25.

B. 23.

C. 27.

D. 21.

Câu 38: Mệnh đề nào sau đây là sai?

A. Nếu\(\int {f\left( x \right)dx = F\left( x \right) + C} \)thì \(\int {f\left( u \right)du = F\left( u \right)} {\rm{ \;}} + C.\)

B. \(\int {kf\left( x \right)dx = k\int {f\left( x \right)dx} } \) (k là hằng số và \(k \ne 0\)).

C. Nếu \(F\left( x \right)\)và \(G\left( x \right)\) đều là nguyên hàm của hàm số \(f\left( x \right)\) thì \(F\left( x \right) = G\left( x \right)\).

D. \(\int {\left[ {{f_1}\left( x \right) + {f_2}\left( x \right)} \right]} dx = \int {{f_1}\left( x \right)dx + } \int {{f_2}\left( x \right)dx.} \)

Câu 39: Kết quả của phép tính tích phân \(\int\limits_2^{{e^2}} {\ln \left( x \right)} dx = {e^a} - a\ln a + b\). Tính \({a^3} + b\).

A. 10.

B. \(9\).

C. \(3\).

D. \( - 7\).

Câu 40: Cho \(({\rm{H}})\) là hình phẳng giới hạn bởi parabol \({\rm{y}} = \sqrt 3 {{\rm{x}}^2}\), cung tròn có phương trình \({\rm{y}} = \sqrt {4 - {{\rm{x}}^2}} \) (với \(0 \le {\rm{x}} \le 2\) ) và trục hoành (phần tô đậm trong hình vẽ).

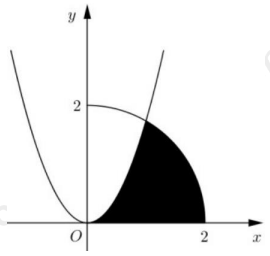
Diện tích của \(({\rm{H}})\) bằng

A. \(\dfrac{{4\pi {\rm{ \;}} + \sqrt 3 }}{{12}}\). 

B. \(\dfrac{{4\pi {\rm{ \;}} - \sqrt 3 }}{6}\).

C. \(\dfrac{{4\pi {\rm{ \;}} + 2\sqrt 3 {\rm{ \;}} - 3}}{6}\).

D. \(\dfrac{{5\sqrt 3 {\rm{ \;}} - 2\pi }}{3}\).

PHẦN II: TƯ DUY ĐỌC HIỂU

Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 10:

ĐÃ ĐẾN LÚC PHẢI TRẢ ƠN CHO ĐẠI DƯƠNG

[1] Hàng thập kỉ qua, bằng cách hấp thụ một phần tư lượng khí CO2 ô nhiễm và hơn 90% nhiệt lượng dư thừa từ hiện tượng nóng lên toàn cầu, các đại dương đã giữ cho nhiệt độ bề mặt đất liền của Trái đất ở mức có thể sống được.

Ảnh: Tình trạng ô nhiễm và đánh bắt quá mức như hiện nay có thể khiến cho lượng nhựa trong các đại dương bằng số lượng cá vào giữa thế kỷ này.

[2] Song, để đáp lại “tấm thịnh tình” ấy, con người lại đổ hàng núi rác thải nhựa xuống biển và đầu độc bờ biển bằng các hóa chất độc hại và những dòng nước công nghiệp.

“Ít nhất một phần ba trữ lượng cá tự nhiên đã bị đánh bắt quá mức, và chỉ còn dưới 10% đại dương là được bảo vệ”, Kathryn Matthews – Giám đốc khoa học tại tổ chức phi chính phủ Oceana chia sẻ với AFP.

“Các tàu đánh cá bất hợp pháp cũng hoạt động mà không bị trừng phạt ở nhiều vùng ven bờ và biển khơi”.

Đồng thời, nước biển cũng bị CO₂ làm axit hóa và những đợt nắng nóng kéo dài nhiều tháng hoặc lâu hơn cũng đang giết chết các rạn san hô – nơi hỗ trợ sự sống cho 1/4 sinh vật biển và cung cấp sinh kế cho 1/4 tỷ người.

“Chúng ta mới chỉ bắt đầu hiểu về mức độ tàn phá của biến đổi khí hậu lên đại dương mà thôi”, Charlotte de Fontaubert, người đứng đầu toàn cầu chương trình nền kinh tế xanh của Ngân hàng Thế giới, cho biết.

Tương lai đáng sợ

[3] Được đồng tổ chức bởi Bồ Đào Nha và Kenya, Hội nghị Đại dương Liên Hợp Quốc kéo dài năm ngày đã quy tụ hàng nghìn quan chức chính phủ, doanh nghiệp, nhà khoa học và tổ chức phi chính phủ để tìm kiếm giải pháp.

Với xu hướng hiện tại, tình trạng ô nhiễm có thể khiến cho lượng nhựa ở biển nhiều ngang với cá vào giữa thế kỉ này. Thông tin ấy đã được đề cập trong chương trình nghị sự của hội nghị, cùng với các đề xuất giải pháp từ tái chế đến cấm hoàn toàn túi nhựa.

[4] Câu hỏi làm thế nào để nghề đánh bắt cá tự nhiên, từ những con tàu chế biến cá của vùng Đông Á cho đến những chiếc thuyền đánh cá dọc theo bờ biển nhiệt đới, trở nên bền vững hơn cũng là một nội dung quan trọng trong chương trình nghị sự của Lisbon.

Và khẩu hiệu mới được đặt ra ở đây là “thực phẩm xanh” – nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng.

Ngành nuôi trồng thủy sản đang phát triển bùng nổ cũng cần phải được theo dõi chặt chẽ bởi nó tiềm ẩn rất nhiều vấn đề từ việc phá hủy các khu rừng ngập mặn quý giá đến việc sử dụng thuốc kháng sinh tràn lan.

XEM TOÀN BỘ ĐỀ